From: Phil

Hi, I am an art student and I am trying to make a "truncated cone" (ie: a cone with the top cut off) out of sheet metal. I need to design a template first and am having problems working out the angles. The truncated cone is 250mm high, 550mm wide at the bottom and 290mm wide at the top. Can you help?

Hi Phil.

The truncated cone is a lot like a lampshade. I've drawn one below with some helping lines labelled t, b, h and w:

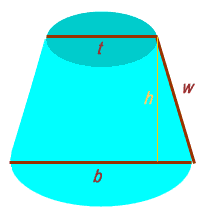So t is the diameter of the circular top of the cone, b is the diameter of the circular bottom, h is the height of the cone and w is the diagonal width. You have measurements for all these except w. What happens if we snip along the line w and unroll it?

A normal (untruncated) cone is made by cutting a sector from a circle and then joining the edges, so we have a pattern shaped like this:

A truncated cone is a normal cone, but with the top cut off. That means the top of the cone (missing in the truncated cone) has a pattern that is cone-pattern shaped. And the truncated cone's pattern, were it not truncated would also be cone-pattern shaped.

Let's look at these cones; they're cut from the same pattern:

So the orange part is the part we are throwing away (truncating) in our truncated cone.

That means our general shape for the pattern of a truncated cone is this:

You can visualize joining the two ends together to make your three dimensional shape. If you refer back to the first diagram I drew and you will see that the width of those ends of the pattern correspond to the line w. The top diameter defines a circle and when we join the ends of the pattern, the inner arc becomes that circle. So the length of the inner arc of the pattern is the circumference of the top circle. The circumference of any circle is 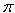times its diameter. So the arc length of the inner circle of our pattern is about 3.1416 times 290 mm, making 911 mm. Similarly, the outside arc is the circumference of the bottom circle of the truncated cone, whose diameter is 550 mm. So the outside arc is 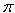times that, making 1728 mm.

Now we need to think about the triangle formed by h and w and the difference between t and b. Look again at my first diagram. By symmetry, the triangle is on both sides of the cone, so we take half of (b - t) as the length of the third side of the triangle. That's (550 - 290) / 2 = 130 mm.

h is given as 250 mm and since this is a right triangle, we can use Pythagorus to solve for w: w² = 130² + 250² , so w = 282 mm. Here's a drawing of what we know so far:

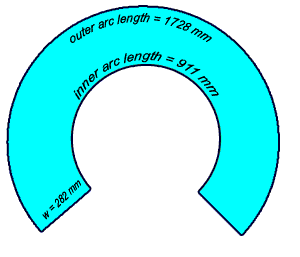More useful dimensions would be the radii of the two circles and the angle of the sector we have cut. First, notice that the outside radius is simply w more than the inside radius. Next, notice that the proportion of the circle cut away from the inner circle is the same as the proportion of the circle cut away from the outer circle (they are, after all, the same cut). That means that the ratio of the arc lengths is the same as the ratio of the full circumference of the two circles! Since the ratio of the arc lengths is 911 / 1728, then the ratio of the circumferences is 911 / 1728. And since the circumference is proportional to the radius, then the ratio of the radii is 911 / 1728.

Now if we express the radius of the inside circle as r and the outside circle's radius is R, then this means r/R is 911/1728. But earlier we said that the outside radius R is simply w more than the inside radius r, so R = r + 282. That means that r/R = r/(r + 282). Now we can simply solve the equation for r:
r/(r+282) = 911/1728

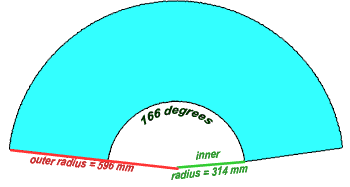
This means r = 314 mm (with rounding).

You also know that R = r + 282, so R = 596 mm.

The full circumference of the inner circle is 2r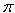, which makes the inner full circumference 2 (314 mm) (3.1416) = 1976 mm. The arc length inside is just 911 though, so we've actually cut away more than half the circle, leaving just 911 / 1976 = 46.1% of the circle. A circle is 360 degrees all the way around, so that means our pattern is just 46.1% of 360 = 166 degrees of arc.

Now we have all the dimensions we need to draw our pattern. Our earlier diagrams were conceptual, but with the figures we have obtained we can now draw a much more accurate diagram:

Hope this helps,
Stephen La Rocque.