 |
 |
|
From: Preston, a student An aircraft going from city A to city B on a bearing of S69 degrees East is traveling at a speed of 430 mph. The wind is blowing out of the north to south at a speed of 25 mph. Find the ground speed and the plane's true bearing.
|
|
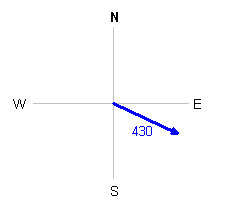
Hi Preston. First, we'll look at how the plane is moving relative to the air around it. That's S69E and 430 mph. Let's draw this:
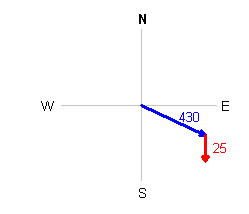
The air is itself moving though. That means we need to add the effect of the wind. We do this by drawing the wind velocity from the end of the airspeed velocity:
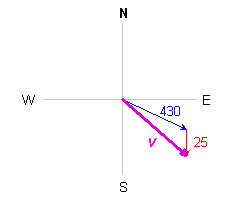
Now the groundspeed and the "true bearing" (aka. the ground bearing) is the sum of these. That means the line that goes from the start of the blue velocity to the end of the red velocity.
Now you have a triangle. You want to know the direction of the purple velocity and its length. Let's redraw this with geometric points labelled.
Law of Cosines: a2 = b2 + c2 + 2bc cos A A second use of the Law of Cosines (using three lengths and solving for the included angle) will give you the Hope this helps, |
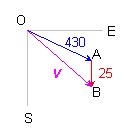Now we can start interpreting things mathematically. The angle 
SOA is 69°. Since AB is vertical (north to south), then 
OAB and their included angle. You can use the Law of Cosines to calculate the length of OB, which is the groundspeed. |
 |
 |