From: Raymond

If I stand on the edge of the sea on a beach and look into the horizon, is there a way or formula for calculating the distance from myself to the horizon?

Do we need to know an angle in order to calculate or is there a formula without needing to know an angle?

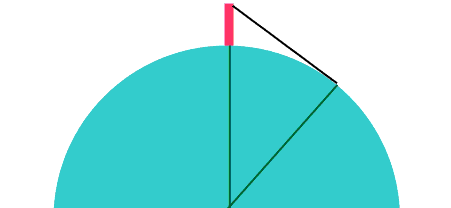
Hi Raymond.

There are at least a couple of approaches to your question ranging from simple to quite complicated.

With a simple approach we consider simply the height of the observer as though standing on a perfect sphere and measure the distance to the tangent point. Here's a diagram that shows this:

Obviously, I've exaggerated the person's height. The person's height (up to eye level) is the red block. The radius of the planet (up to sea level) are the green lines. The black line is the sight-line to the horizon. The arc under the sight-line is the surface distance between the viewer's feet and the horizon point.

With realistic figures for the radius of the earth (6380 km) and a viewer's eye-height (155 cm), we can calculate the unknown lengths in the diagram.

First we use Pythagorus to calculate the length of the sight-line, because the tangent line to a circle makes a right angle with the radius.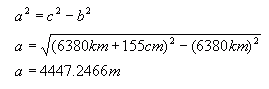

So that's the sight-line. The viewer can see about four and a half kilometers. Let's take a look at the surface distance. That's the arc length from the viewer's feet to the horizon point. Remember that arc length is simply the radius times the angle when measured in radians:

We know the radius, but we need to calculate that angle though: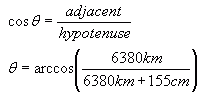

(Remember that we need to be working in radians when we do this arccos!) Now that we have an expression for the angle, we can substitute it in and calculate the arc length: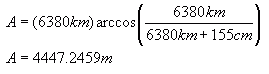

Well, you can see when you compare this to the sight-line there is not much difference at all! That's because of the huge difference between the radius of the earth and the height of the viewer.

That's the "simple" answer to your question. The more complicated answer involves more realistic physics concepts. There are a lot of directions we can take this. The earth is not a perfect sphere, so it depends on where the viewer is and in what direction he or she is looking. Waves can be quite high. If there is a two meter swell one kilometer offshore, the viewer won't see past that swell (it will appear to be the horizon). Then we get into atmospheric optics...

I'm sure you've heard of light refraction (that's what gives us mirages). It is due to the density of the atmosphere (generally most dense closest to the surface of the earth). There's a very detailed discussion of this on this external link to refraction discussion. Typically, this might be on the order of a 15% bonus in distance, but with thermal inversions, some viewers on ships have reportedly seen mountains 750km away! From an atmospheric optics perspective, this is certainly possible.

Hope this helps,
Sue