My Name is Ronald. I have a building block of land with four unequal sides and only one right angle. I want to know the total area (in metres) and how the calculations were carried out.

The four sides are: Rear of property: 9.14 metres
left side: 36.9 metres
Right side: 32.61 Metres
front to street: 27.43 Metres

The front to street and right side constitute a right angle. but there are no others.

I am attaching a plan that shows the area and shape that might serve to assist in the calculations.

Regards,
Ronald

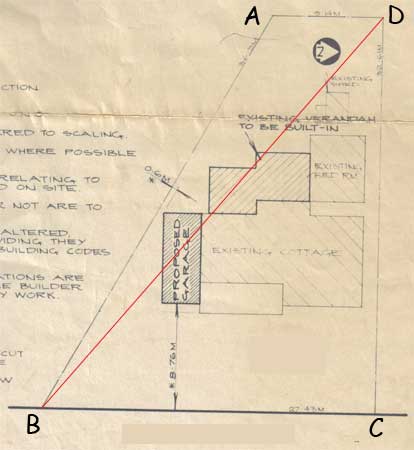
Ronald,

Below is part of the plan you sent. I added one line and labeled the corners of the lot.

Since the angle at C is a right angle the length of CD is the height of triangle DBC and hence you can find its area using the standard expression

area of DBC = ¹/₂ base height = ¹/₂ 27.43 32.61 = 447.25 square metres

Again since the angle at C is a right angle I can find the length of DB using Pythagoras theorem.

|DB|² = |BC|² + |CD|² = 27.43² + 32.61² = 1815.81

and hence

|DB| = √1815.81 = 42.61 metres.

Finally since I now know the lengths of the sides of triangle ABD I can find its area using Heron's Formula.

a = 42.61 metres, b = 9.14 metres and c = 36.9 metres

and hence

s = (42.61 + 9.14 + 36.9)/2 metres

and

area of ABD = Sqrt[s (s-a) (s-b) (s-c)] = 140.92 square metres.

Thus the area of your lot is

447.25 + 140.92 = 588.17 square metres.

Penny