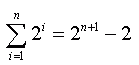From: Sharon, a college student

Prove by induction for n > 1:
          

 

Hi Sharon.

With proofs of this nature, always start by trying the first value manually if you can. That would be n = 2. Let's start with the left-hand-side (LHS) of the theorem you are asked to prove: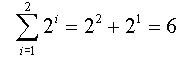

Now let's look at the RHS:

Good, they both equal six. So you can say that this much is true:

for some

In particular, you know it is true for: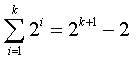

Now what you want to show is the inductive step. You want to prove that if that last statement is true (and you know it is), then:

must equal

So let's get started with what we know: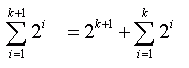

That's clear enough - all we did was wrote out the extra term explicity, but now we use what we stated before and substitute for the second summation: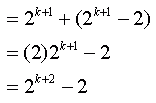

Which is just what we wanted to prove. So we've said that if it is true for one value of k, it is true for the next (and the next...). Since we've shown it is true for k = 2 earlier, we know it is true for all larger integer values of k, which is the same as saying it is true for n > 1, as required.

Hope this helps!
Stephen La Rocque.