From: Skye

Hello guys. I really need help with this sequence problem and im wondering if you could help.

If the 1st, 4th, and 8th terms of an arithmetic sequence are in a geometric sequence, find the common ratio of the geometric sequence.

I really don't understand this! How can you get the ratio if they don't give you any numbers? please help!

Hi Skye.

Maybe your trouble lies in an unstated assumption in the question. I'll re-write the question with the assumption plainly shown:

If the 1st, 4th, and 8th terms of an arithmetic sequence are consecutive terms in a geometric sequence, find the common ratio of the geometric sequence.

Now is it easier to understand? Here's how I would solve the problem (no, you don't need the values of the terms themselves!)

First let's think about Arithmetic Sequences. An Arithmetic Sequence is one where there is a constant difference between consecutive terms. We don't know the difference, but let's call it D. We do know that if we call the first term of the sequence A, then the second term is A + D and the third term is A + 2D, etc.

This means that the first, fourth and eights terms in the arithmetic sequence are A, A + 3D and A + 7D.

Now we are (implicitly) told that these are consecutive terms in a geometric sequence. A Geometric Sequence is one where there is a constant ratio between consecutive terms. We want to know this ratio. Let's call it R. So if G₁ is the first element in the geometric sequence and G₁ is the second and G₃ is the third, then: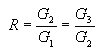

But remember that the question indicates that we can take: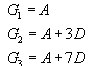

So substituting these values into the constant ratios equation, we get: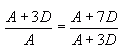

Now this is an equation in two variables. Can you simplify this? You should be able to come up with an expression that defines A in terms of D (that is, simplify and re-arrange this equation to solve for A).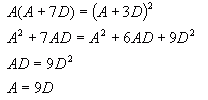

Now let's substitute that into the equation for R to get our final answer: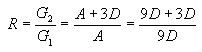

And I'm sure you can take it from here! :)

Hope this helps,
Stephen La Rocque.