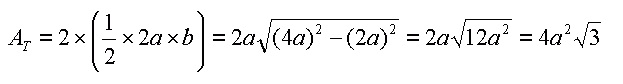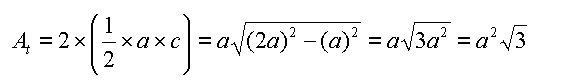An equilateral triangle and a regular hexagon have equal length perimeters. What is the ratio of their areas?

Our teacher has asked us to do this...I think I can find one solution as a hexagon will be made up of 6 equilateral triangles and if the hexagon and triangle have equal perimeters then the triangles in the hexagon will have 1/2 the area of the larger triangle. As there are 6 of the smaller triangles the total area of the hexagon in relation to the triangle will be 6 x 1/2 or 3. So the ratio of the area of a hexagon and a equilateral triangle with equal perimeters is 3:1

are there any other ways to solve this problem?

thank you
Trevor

 

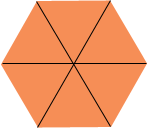
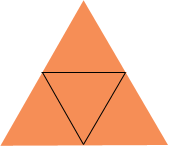
I have two solutions for you.

Trevor,

I like the way you have approached this question but I have a problem with the details. A regular hexagon is made up of 6 equilateral triangles

and each of these triangles has half the perimeter of the hexagon and hence half the perimeter of the larger triangle. But why half the area?

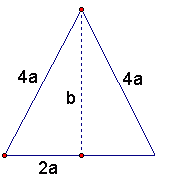
Penny

Hi Trevor. Here is a solution using some algebra. Let's try figuring out the ratio using perimeter of 12a and see if we get the same ratio as you predicted. I used 12a as it makes some of the expressions come out neatly. Let's draw the triangle:

Each side is 4a. We can see that the area of the equilateral triangle is twice the area of a smaller right triangles. The right triangle's area is 1/2 base x height, and the height (b) is obtained through Pythagorus' Theorem from the other two sides. If we put that all together, we get:

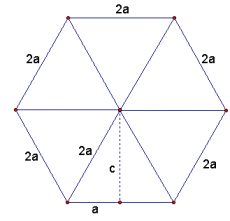
Now let's look at the hexagon. You are right that it is made up of six equilateral triangles, so each side is 2a this time:

Using the same logic as before, let's calculate the area of each small equilateral triangle:

We can see by this that the ratio of At is not half of AT, it is  1/4 instead! Now when we look at the ratio of the area of the hexagon to the area of the large triangle, we get:

I hope this helps!
Stephen La Rocque>