How do you the Pythagorean relation to find the length of the hypotenuse x to one decimal place?

x² = 3.6²+ 5.3²

My teacher, Mr. Mutrie, wants to know what this means?

SOH CAH TOA

Hi Vicky,

I expect that you have a triangle with two sides of lengths 3.6 units and 5.3 units, and there is a right angle at the vertex where these two sides meet. If the third side (the hypotenuse) has length x units then the Pythagorean Theorem states that

x² = 3.6²+ 5.3²

To find x you need to perform the calculations to get

x² = 3.6²+ 5.3² = 12.69 + 28.09 = 40.78

Thus

x = √40.78 = 6.386

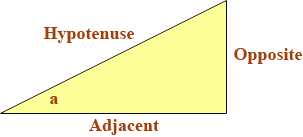
Since you are asked to express x to one decimal place, x = 6.4

SOH CAH TOA is a memory device to help you remember three of the trig functions. Sometimes these memory devices are helpful. I use "Man very early made jars stand up nearly perpendicular" to help me remember the order of the planets. The three you ask about, SOH CAH TOA, I find no easier to remember than the functions themselves.

In a right triangle specify one of the non-right angles. I am going to call the measure of this angle a degrees. The three sides of the triangle are the hypotenuse, the side opposite to a and the side adjacent to a.

The three trig functions sine, cosine and tangent are defined by

Sin(a) = Opposite/Hypotenuse (SOH)
Cos(a) = Adjacent/Hypotenuse (CAH) and
Tan(a) = Opposite/Adjacent (TOA)

I hope this helps,
Harley