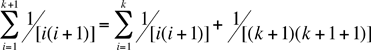Question: how do i prove by induction on n that
n
∑ 1/i(i+1) = n/(n+1)
i=1

for all positive integers n

Victoria,

There are two steps in a proof by induction. The first is to verify that the statement is true for the smallest value of the index n, in this case it is n = 1.

1
∑ 1/[i(i+1)] = 1/[1(1 + 1)] = 1/2 and n/(n + 1) = 1/(1 + 1) = 1/2
i=1

Hence the statement is true for n = 1.

The second is to show that if the statement is true for any particular value of n then it is also true for the next value of n. To do this I am going to assume that the statement is true for the particular value n = k. That is I assume that

k
∑ 1/[i(i+1)] = k/(k+1)         equation 1
i=1

and I want to prove that it is true for the next value of k. Thus I need to show that

k+1
∑ 1/[i(i+1)] = (k+1)/(k+1+1)         equation 2
i=1

Here is how I would start this proof.

But from the assumption (equation 1) this can be rewritten

k+1
∑ 1/[i(i+1)] = k/(k+1) + 1/[(k+1)(k+2)]
i=1

Can you simplify this to get (k+1)/(k+2)? If so you will have verified that equation 2 is true and hence, by induction, you have a proof that

n
∑ 1/i(i+1) = n/(n+1)
i=1

is true for all positive integers n.

Penny