Name: Amy

Who is asking: Student
Level: All

Question:
What is an order relation?

An order relation is a relation, that is, a criterion of comparison between objects, which satisfies the properties of reflexivity, antisymmetry and transitivity.

Common examples are the relations "is larger than or equal to" and "is a divisor of" between integers, and the relation "is an ancestor of" between people (if we set the convention that every individual is an ancestor of itself).

The property of reflexivity is the property that every element satisfies the comparison criterion when compared to itself: Every integer is larger than or equal to itself, therefore the relation "is larger than or equal to" is reflexive. Similarly, every integer is a divisor of itself; therefore "is a divisor of" is reflexive. And every individual is an ancestor of itself (according to our convention) therefore "is an ancestor of" is reflexive.

Antisymmetry is the property that if an element satisfies the comparison criterion when compared to a second element, then the second cannot satisfy the comparison criterion when compared to the first, unless they are really the same element: If an integer is larger than or equal to a second integer, then the second integer cannot be larger than or equal to the first, unless they are the same. Similarly, if a number is a divisor of a second number, then the second number cannot be a divisor of the first, unless they are the same. And finally, if an individual is an ancestor of a second individual, then the second cannot be an ancestor of the first, unless they are the same. Therefore our three relations are antisymmetric.

Transitivity is the property that if a first element satisfies the comparison criterion when compared to a second element, and this second element satisfies the comparison criterion when compared to a third element, then the first element satisfies the comparison criterion when compared to the third element. This is true for our three relations: If an integer is larger than or equal to a second integer, which in turn is larger than or equal to a third, then the first integer is also larger than or equal to the third. Also, if an integer divides a second integer, and this second integer divides a third integer, then the first number divides the third. And finally, if an individual is an ancestor of a second individual, which in turn is an ancestor of a third individual, then the first individual is an ancestor of the third.

We commonly use mathematical notation to describe an order relation. If you use the letters a, b and c to represent the objects being compared and to represent the relation then the three properties can be written:

• Reflexivity: For each a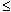, a a
  
  
• Antisymmetry: For each a and b, if a 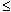b and b 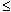a then a = b.
  
  
• Transitivity: For each a, b and c, if a 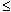b and b 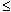c then a 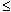c
  
  

Any relation that satisfies the three properties of reflexivity, antisymmetry and transitivity is an order relation; there are many other examples. Can you think of any?