Subject: interest rate
Hi, my name is anthony.
This question is base on my interest. I would like to know the formula
for calculating this example: If you borrow $10,000 from a bank with an
APR of 11.7% to be paid off in 5 years, what is your monthly payment?
Could you please show me step by step how this formula is developed.
Thanks!
I think that what you are looking for is called amortizing the loan. I want to illustrate the method with a smaller example. Suppose that I borrow $1,000 for 6 months at an annual interest rate of 12%. I have calculated the monthly payments to be $172.55. (I know that the calculation of the monthly payment is your question and I will return to it later.) The payment schedule is in the table below.
| Month | Payment | Interest | Applied to Principle | Unpaid balance |
|---|---|---|---|---|
| 1 | $172.55 | $10.00 | $162.55 | $837.45 |
| 2 | $172.55 | $8.37 | $164.18 | $673.27 |
| 3 | $172.55 | $6.73 | $165.82 | $507.45 |
| 4 | $172.55 | $5.07 | $167.48 | $339.97 |
| 5 | $172.55 | $3.40 | $169.15 | $170.82 |
| 6 | $172.55 | $1.70 | $170.85 | $0 |
The reasoning behind the schedule above is the following. At the first of month 1 I have borrowed $1,000 at 12% per year. Hence in one month the interest owing will be one-twelth of 12% of the principle which is $1,000. Thus the interest owing is 0.12/12 x $1,000 = $10.00. Hence $10.00 of the $172.55 payment goes toward the interest and the difference, $162.55, is applied to the princple. Thus at the beginning of month 2 I owe $1,000 - $162.55 = $837.45.
Thus in the second month I have borrowed $837.45 and hence owe 0.12/12 x $837.45 = $8.37 in interest. Therefore $8.37 of my $172.55 payment goes to interest and the remainder, $172.55 - $8.37 = $164.18 goes toward he principle. Thus at the beginning of the third month I owe $837.45 - $164.18 = $673.27.
This procedure continues for 6 months when the unpaid balance is $0. (The difference between $170.82 and $170.85 is roundoff error.)
The procudure to calculate the monthly payments for your loan of $10,000 at 11.7% per year for 5 years is as follows. Assume that the payment is $M per month. Complete the 60 rows in the table above that correspond to 5 years. In each of the 60 rows the Unpaid balance column will be an algebraic expression involving $M. The expression in the Unpaid balance column and the sixtieth row must be zero so set the exprression equal to zero and solve for $M. The result is the following formula for $M.
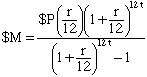
For your situation the monthly payment is
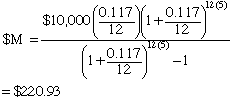
Penny