hi, my name is Becky, my question is:

What are all the real values of x that are solutions for the inequality [x-2] < 6? ( it's less than or equal to)

What is the distance between the points with (x,y) coordinates (3,-2) and (-3,-1)?

Thanks,

I am not sure how you are using the square brackets in your first problem. If they are just acting as brackets then the solution would be obtained by adding 2 to each side of the inequality.

So the answer is all numbers x which are less than or equal to 6.

I think however that you might be using square brackets to designate absolute value, that is [x-2] = |x-2|. If this is what you mean then my solution would be to interpret |x-2| as the distance between x and 2 and think of the question geometrically. If |x-2| is less than or equal to 6 then x can't be more than 6 units to the right of 2 or 6 units to the left of 2.

From the diagram it is clear that x can be any number between -4 and 8, that is x is any number that satisfies -4<=x and x<=8.

For your second problem I would again draw a diagram and this time use the theorem of Pythagoras

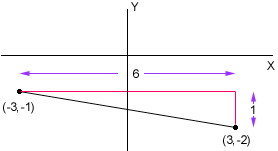
The triangle in the diagram is a right triangle so the length of the hypotenuse (distance between the points) is the square root of 6² + 1²

There is an algebraic formula for the distance between points in the plane but it is just an algebraic way to express the theorem of Pythagoras.