My name is Corinne and I am a junior in high school and i am taking a pre calculus class. This is a secondary problem.
A family is traveling due west on a road that passes a famous landmark. At a given time the bearing to the landmark is N 62 degrees W, and after the family travels 5 miles farther the bearing isÊN 38 degrees W. What is the closest the family will come to the landmark while on the road?
this problem uses the law of sines but i don't know how to draw the picture. the answer in the back of the book is 4.55 miles.
Hi Corinne,
The bearing of N 62 degrees W tell you to look North and then rotate 62o toward the West as in the diagram.
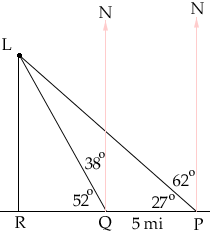
In the diagram R is the closest point on the road to the landmark, so angle LRP is a right angle.
In triangle LQP you know two of the angles, 27o and 38o + 90o = 128o so you can find the remaining angle PLQ. Use the Law of Sines to find the length of LQ and then you can find the length of LR since sin(52o) = |LR|/|LQ|
Cheers,Harley