Sender: corrie
Subject: calculus question

hi! i have a question i was hoping you could help me with!

I need to find if the mean value theorem exists. and if so, find all values c guaranteed by the theorem.

f(x) = |x2-25| on the interval [-10,0]

thanks for your time and help!

corrie
secondary student

Hi Corrie,

For the Mean Value Theorem to apply you need f(x) differentiable in the interval (-10, 0). My first thought is to sketch the graph of the function

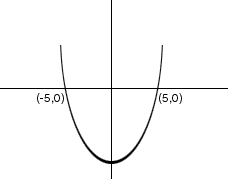
f(x) = |x2-25| The function g(x) = x2-25 is a parabola that opens upward and crosses the X-axis at the points where x2-25 = 0, that is where x = 5 and x = -5. The graph is

y = x2-25

When you take the absolute value of the y-values to get the function f(x), the negative y-values become positive. Thus the part of the graph below the X-axis gets "turned over" and the graph becomes


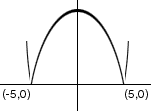
y = |x2-25|

At the point (-5, 0), which is inside the interval (-10, 0) the curve clearly has no tangent line. Thus y = f(x) is not differentiable at x = -5 and thus the Mean Value Theorem does not apply.

Cheers,
Harley
Go to Math Central