Subject: Complex help needed

Please can somebody help me. I am having enormous difficulty with one question in my maths homework. The question is shown below. If anybody out there can find the answers and show the workings and help me to understand.

(a) Solve the equation

where z is a complx number, expressing your answer in the form a + ib

(b) Find the square root of 5 + 12i and hence the square root of -20 - 48i

(c) Use the results of (b) to solve the quadratic equation

Hence factorise the expression

For a I would first multiply both sides by 45 + 4i to get

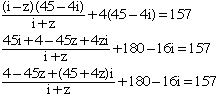
Now multiply through by i+z and collect all the terms containing z. The resulting expression will be of the form

and divide both sides by (p + iq) to get

Finally multiply the numerator and denominator of the right side by (p - iq) to get

and simplify.

For b), if a + ib is a square root of 5 + 12i where a and b are real, then (a + ib)(a + ib) = 5 + 12i. That is

Hence

Solve these two equations for a and b.