Subject: Rationale for Problem presented in Parade by Marilyn Vos Savant
Problem: Two ferry boats leave from opposite shores. One is faster than the other. They meet 720 yards from the nearest shore. They proceed to destination and upon returning they meet 400 yards from the other shore. What is the exact width of the river. The answer is 1,760 yards. Why? Thanks in advance for any help you can give as an explanation.
Gil Edwards
retired teacher
Hi Gil,
I need to introduce some notation to talk about the diagram. Suppose boat A leaves from P, boat B leaves from Q and they meet for the first time at R which is 720 yards from P.
I want to call the time it took 1 time unit. Thus in 1 time unit the total distance travelled by the two boats was 1 "river width".
They continue on as in the second diagram and meet for the second time, 400 yards from Q.
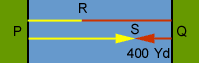
Notice from the diagram that, since they left R, they have traveled a total distance of 2 "river widths". Thus the time since they left R is 2 time units. Since boat A travelled 720 yards in 1 time unit, it travelled 2(720) = 1440 yards in two time units. Hence |RQ| + |QS| = 1440 yards.
Since |QS| = 400 yards, |RQ| = 1040 yards and thus 1 "river width" = |PR| + |RQ| = 720 + 1040 = 1760 yards.
Cheers,Penny