Subject: Circle Problem Driving me mad...

Christopher
Grade 10 Student

Attached to this email is the diagram that goes with my problem.

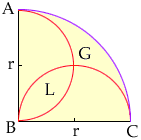
Inside the quarter-circle are two semi-circles with the same radius, (r). Which has a greater area, G or L?

Thanks in advance.

You can write the area of the quarter-circle since you know its radius is 2r. You can also write the areas of the two semi-circles since you know each has radius r. The result follows from the observation that the area of the quarter-circle ABC is equal to the area of the semi-circle on AB plus the area of the semi-circle ob BC minus the area of L plus the area of G. (You need to subtract the area of the region L since in adding the areas of the two semi-circles you included L twice.)