My name: Jacky
Level of question. Grade 10-11 Secondary school
Who is asking the question: Student

I just saw a problem one day in the textbook in which our teacher says it is a problem slightly harder than grade 10 level.

Here is the problem: (It is more helpful to draw a diagram) A square with a dimension 20 by 20cm. and a quarter of the circle with the radius of 25cm (A quater of a circle is created by 2 cuts that are perpendicular bisectors of each other where the intersecting point is at the centre of the circle). With these 2 pieces, the 2 pieces are placed over each other in which the 90^o angle of the quarter circle matches with one of the right angles on the square. Now, calculate the overlapping area of the 2 figures.

Thanks for taking the time to think about this question.

I think that the problem is a little harder than the grade 10 level as I think you need to use some trigonometry to solve it.

The overlapping region (the part shaded yellow in the diagram) can be seen as two triangles (ABF and AEC) and a sector of a circle (ACB).

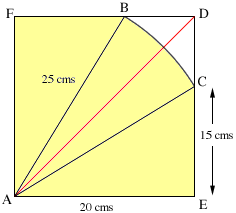
Each of the triangles has area 1/2 x base x height = 1/2 x 20 x 15 = 150 square cms. and hence the area of the two triangles is 300 square cms.

The area of a sector of a circle is

where theta is the angle at the center of the circle measured in radians. Divide the sector in half by the line from A to D and then the area of the sector is

Fianlly angle DAC = angle DAE - angle CAE.

Angle DAE is 45^o or in radians pi/4. The easiest way to describe angle CAE is to use trigonometry and say that it is the angle whose tangent is 15/20 = 3/4. This angle is sometime written arctan(3/4). Thus the area of the overlapping region is

which is approximately 388.69 square centimeters.