Name: Jacky

Question: I was searching on the web and I came accross this problem The only way I could think of is to plot the vertices of the rhombus onto a grid paper and calculate it. However, this is kind of slow, is there an easier way or another way to do it?

Here is the question..
A rhombus ABCD is drawn in which the diagonals are 12 and 20 units long. A circle is inscribed in the quadrilateral with the centre of the circle right on the intersection point of the 2 diagonals. The circumference of the circle touches all 4 sides of the rhombus. Is it possible to find the radius of the inscribed circle? If so, how and what is it?

The diagonals of a rhombus are perpendicular, so ABO is a right triangle with right angle at the center O. The legs are 6 and 10, so the hypotenuse AB has length sqrt(136).

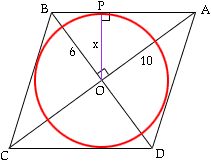
The radius you seek is the perpendicular OP from O to AB. Suppose that |OP| = x and use similar triangles to get x:10 = 6:sqrt(136). x is 30/sqrt(34), which is about 5.145.