Level of question:Secondary

Question:
A rare disease infected 1 in 1000 people in the population. A test for the disease is accurate 99% of the time when given to an infected person and also when given to a heathy person.

1. Fill out a two-tier tree diagram and find the probability of the false positive(i.e the conditional probabily of being healty even when tested postive by the test) Comment on the result?
    
   
2. John after tested once positive was tested again .Fill out completely a three -tier diagram and find the probabilty of false double-positive(ie. the conditional probabily of healthy even john was tested positive twice) what is the probability of a person being healthy and twice-positively tested?

Thankyou for your kindy help!!

Yours sincerely
James

I used the letter I to designate infected, H to designate healthy, P to designate a positive test and N to designate a negative test. The two-tier tree diagram is then

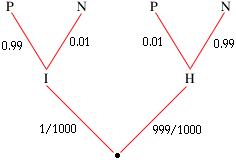
The probability of a false positive is the conditional probabily of being healty even when tested postive by the test, that is Pr(H|P). Thus to find the probability of a false positive you need to calculate:

From the tree diagram

You can receive a positive test by either being healthy and receiving a positive test or being infected and receiving a positive test. Thus:

Hence the probability of a false positive is:

Now put a third tier on the tree diagram to answer part 2.