This is either a level 9-12 geometry question or a graduate level math theory question. I am an engineer not specializing in surveys and geometry. Apparently, I need to touch up on my geometry.
I have a 5 sided irregular polygon I am trying to figure out the area of. There are no right angles in the polygon as far as I can tell. I do not know any angles.
The sides are of lengths (in feet)
51.13
239.37
120.0
200.0
216.59
Any help would be greatly appreciated.
Jason
The lengths of the sides do not determine the pentagon's shape. The area
could be any number between 0 and some maximum value that occurs when the
vertices lie on a circle. Just think of the polygon as as five rods connected that are hinged at the ends. There is a device that you can run around the
perimeter of the polygon that gives you an approximate value for the area.
Perhaps you have access to a computer version of that device. Otherwise, the lengths of the 2 diagonals from one of the vertices can be used to partition the polygon into three triangles.
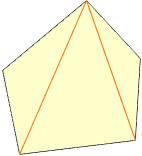
You can then use Heron's formula three times. Heron's formula
Chris