1. Graph each function and state its domain and range. y = 3x2 + 4

  2. For each parabola find: i) the direction of opening
    ii) the coordinates of the vertex
    iii) the y-intercept
    iv) the x-intercepts     y = x2 + 3

  3. Find the equation of each parabola vertex at (0, -2) and passing through the point (3,7)

Kathleen Hi Kathleen,

  1. To plot the graph first calculate some values and record them in a table



    xy
    04
    17
    216
    331
    -17
    -216
    -331


    Plot the points on the graph and join them. I have joined the points with straight lines but you should join them with a smooth curve.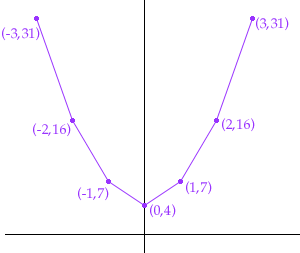

    From the table you should see that any value of x will yield a valid value for y so the domain of the function is all real numbers. From the table and the graph you can see that the y-values are all greater than or equal to 4. Thus the range of the function is all real numbers which are greater than or equal to 4.

  2. If you plot the function y = x2 + 3 as in 1. you will see that the parabola opens upward and the vertex is at the point (0,3). This is the only point where the graph crosses the y-axis so the y-intercept is 3. The graph never crosses the x-axis so there are no x-intercepts.

  3. It is difficult to solve this problem without seeing the text book. I am going to assume that the text has two types of parabolas,

    y = a x2 + b and x = c y2 + d (The notation might be different.) The first opens upward (North) if a is positive and downwards (South) if a is negative. The second opens to the right (East) if c is positive and to the left (West) if c is negative. You might however have a parabola that open to the North-East or South by South-West, etc. However with the assumption that the only parabolas of interest are of the two types above I would proceed as follows.

    Assume the parabola is of the form y = a x2 + b. Since it passes through (0,-2) and (3,7) these points satisfy the equation. Thus

    -2 = b and 7 = 32 a + b Thus 7 = 9 a -2
    9 = 9 a
    a = 1     Thus the equation is

    y = x2 - 2

    If the parabola is of the form x = c y2 + d then again (0,-2) and (3,7) satisfy the equation so

    0 = 4 c + d and 3 = 49 c + d Subtracting the first of these equations from the second gives 3 = 45 c and hence c = 1/15. Substituting c = 1/15 into -2 = 4 c + d gives d = -4/15. Thus the equation is

    x = 1/15 y2 - 4/15

Cheers
Harley
Go to Math Central