Name: Kumar
Who is asking: Other
Level: All
Question:
In a Pyramid OABC, all the three sides of the base: a, b, c are known. Also known are the angles between the three sides from the vertex O: Angles AOB, BOC, COA.
With this information, is it possible to calculate the lengths of the three sides: OA, OB & OC.
Hi Kumar,In a sense YES, it is always possible to calculate the lengths, but it might turn out that no pyramid satisfies the given conditions, or there might be more than one pyramid that works. For a simple example to get an understanding of the problem, take all the angles to be 60 degrees. Fix a = 1, b = c, and let b take on different values. (Think of the pyramid lying on the face BOC with the edge OA along the line L that forms the appropriate angles.)
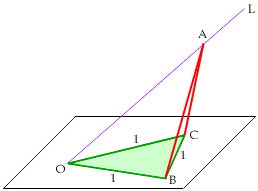
You can imagine the edge BC to be a hinge so that triangle ABC forms a flap. When b = c is greater than or equal to 1 the flap will have a unique point A on L where it closes (and there will be exactly one pyramid with the given parameters).
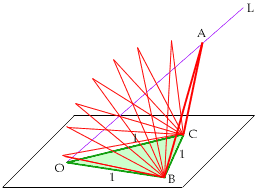
When b is slightly less that 1 there will be two positions for A on L (and there will therefore be two pyramids).
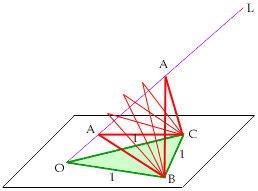
When b is very small, the flap will not reach L and no pyramid will exist.
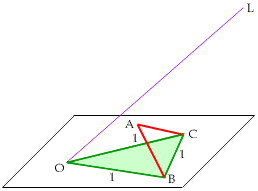
It is probably not hard to adjust the relative sizes of b and c to get up to 8 pyramids (keeping the given angles fixed at 60 degrees), but I have not tried it. If you prefer an algebraic approach, you could let x = OA, y = OB, and z = OC. The cosine law then gives you three quadratic equations in x, y, and z, such as a2 = y2 + z2 - 2yz*cos(BOC). This is sufficiently hard to solve even in the special case when the three angles are 60 degrees, when the equations look like, a2 = y2 + z2 - yz.
CheersChris