Hi, my name is Sarah, and I'm asking this question on behalf of niece who is in secondary two. Thank you.

Q1. What is the angle formed by the hour hand and the minute hand of a 12 hour clock at 5.50pm.

Q2. Two pipes of different sizes are used to fill a water tank. The smaller pipe takes 5 hours to fill the tank alone and the larger pipe takes 3 hours to fill the tank alone. How long will the tank be filled if both pipes are used at the same time ?

Q3. The area of a circle is twice the area of a square. Find the ratio of the perimeter of the circle to that of the square.

Q1. I am going to measure the angle from the minute hand to the hour hand in a counterclockwise direction.

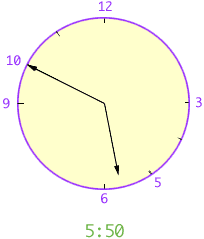
The angle between the minute hand and the 12 position on the clock face is two-twelfths of 360^o. The angle between the 12 position on the clock face and the 5 position on the clock is five-twelfths of 360^o (this would be the position of the hour hand at 5:00). In the 50 minutes between 5:00 and 5:50 the minute hand has moved ten-twelfths of the way around the clock face and the hour hand has moved ten-twelfths of the way from 5 to 6, that is ten-twelfths of, one-twelfths of 360^o.Thus the angle between the minute hand and the hour hand is

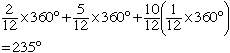
Q2. Look at the rates that each pipe fill the tank. The smaller pipes is running at 1/5th of a tank per hour and the larger pipe is running at 1/3rd of a tank per hour. Thus together they are running at (1/5 + 1/3) = 8/15th of a tank per hour.

Q3. If the circle has radius r and each side of the squarre is of length q then the first sentence says pi r² = 2 q². The ratio of the perimeter of the circle to that of the square is (2 pi r)/(4q). Use the equation in the previous sentence to write q in terms of r and then substitute this value into the ratio expression.