The following problem was given to grade eleven algebra students as a homework assignment. To manufacture cushions and pillows, a firm uses two machines A and B. The time required on each machine is shown. Machine A is available for one full shift of 9.6 hours. Machine B is available for parts of two shifts for a total of 10.5 hours each day.

Iten	   Machine A	Machine B
Pillows	   3 minutes	5 minutes
Cushions   8 minutes	6 minutes

Display graphically all possible answers for these restraints. How many of each type should they make per day in order for the manufacturers to maximize profit, if the profit made on each cushion is $3.20 and on each pillow is $1.85? What is the macimum profit?

My common sense answer that you would use A to make pillows only and B to make cushions only is supported by feeding all the data into a spreadsheet.

a) Is this conclusion correct?
b) Can anyone help to explain how this would be done using algebra?

Fiona McPhee (substitute teacher)

This is a problem of a type called a linear programming problems. They are characterized by linear constraints and a linear function to optimize within these constraints.

Let X be the number of pillows manufactured and Y the number of cushions manufactured. It takes 3 minutes/pillow to manufacture a pillow on machine A and 8 minutes/cushion to manifacture cushions on machine A. Since Machine A is only available for 9.6 hours (that is 9.6x60 = 576 minutes), we know that

Likewise, from machine B

These two inequalities are constraint conditions. There are two other constraints, X and Y are both non-negative. That is

You can then plot the lines

to will see the region in the plane, called the feasible region, where (X,Y) can fall if X and Y are to satisfy the constraints. (You need to solve the first two equations to find the point (72,45).)

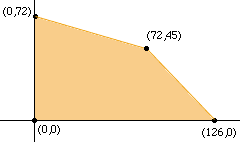
The final step is then to maximize the profit function

subject to the condition that (X,Y) is in the constraint region.

Rewrite the profit equation

This is a family of parallel lines in the plane with Y-intercepts P/3.2. Two of these lines, P = $300.00 and P = $200.00 are plotted in red on the diagram below.

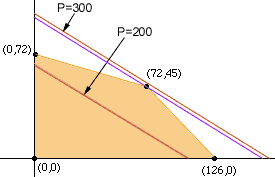
From the diagram you can see that no pair of numbers (X,Y) in the feasible region produce a profit of $300 while many points (X,Y) in the feasible region produce a profit of $200. Increase P from $200 the until the profit line passes through the point (72,45). This is the maximum value that P can attain, as any further increase in P produces a profit line that does not intersect the feasible set. Thus the maximum value of P is the value which assures that (72,45) is on the profit line. That is the maximum value of P is