Name: nishi
Who is asking: Student
Level: Secondary
Question: how do i prove (a simply as possible) why the bond angles of a tetrahedral polygon are 109.5 degrees? *i already have two explanations that i don't understand. one is about "theory of dot products" and "vectors" and a hook-like symbol w/ a cosine, and the other has an incomprhensible diagram w/ difficult notation- PLEASE BE SIMPLE! thanks sooo much
Hi Nishi,
Imagine that you create the tetrahedron by joining opposite vertices on the faces of a cube as in the diagram below. To simplify the arithmetic assume that the cube has sides of length 2.
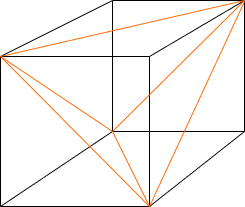
Let O be the point at the center of the cube (equidistant from the eight vertices) as in the diagram below. Construct the triangle OPQ.
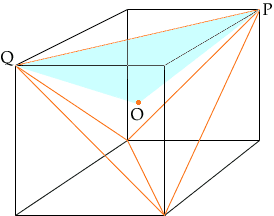
Consider the triangle OPQ. Let R be the midpoint of PQ.
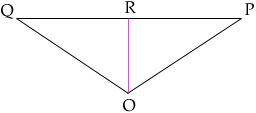
Since the sided of the cube are of length 2, a use of Pythagoras' Theorem gives |PQ| =
. Also, since O is at the center of the cube, |OR| = 1. From the diagram the tangent of the angle ROP is 
. Thus
) = 109.5o
Harley