Subject: Integral Calculus problem
Dear Sir:
A fellow teacher asked me about a problem she wanted to give to her students. It involved whether to take a million dollars or a penny doubled a number of times. I was able to determine the number must have been .01 * 230 which is about $10 million and a lot more than $1 million. Then I reasoned, what about the doubling from 1 - 29. I reasoned that since each amount would be half the previous, the total amount would be the same as
To check that I was right I used a spreadsheet and did a Riemann sum.
| 1 | $0.01 |
| 2 | $0.02 |
| 3 | $0.04 |
| 4 | $0.08 |
| 5 | $0.16 |
| . | . |
| . | . |
| . | . |
| 29 | $5,368,709.12 |
| 30 | $10,737,418.24 |
| _________________ | |
| Total | $21,474,836.47 |
When I finished I reasoned that I had done the task in several steps and I could have done it in 1 step. Thus I integrated .01 * 2x from 0 through 30 but the number I got was $15,490,820.0324. [.01 * (1/ln 2)(230 - 20)]. I then used the finite integral on my graphing calculator and got the same number. I have been unable to figure out why I don't get the correct answer by integration. I have asked a couple of other math teachers but no one has been able to give me an answer.
Yours truly,
Douglas Norberg
Hi Douglas,I want to do this with fewer time intervals (only 5) and make the units cents rather than dollars to eliminate the decimals. This gives
| 1 | 01 |
| 2 | 02 |
| 3 | 04 |
| 4 | 08 |
| 5 | 16 |
| _________________ | |
| Total | 31 |
or using your algebraic exprression
In this case the integral of 1 * 2x from 0 through 4 is 21.64.
The cause of the discrepancy can be seen in the diagram. The blue rectangles each have a base of 1 unit and a heights of 20 = 1, 21 = 2, 22 = 4, 23 = 8, and 24 = 16, for a total area of 31 square units. However the integral of 1 * 2x from 0 through 4 is is the area under the curve in black from 0 to 4; a value of 21.64.
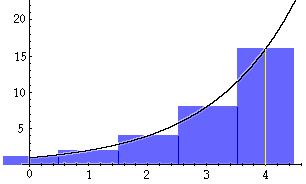
The largest difference between the two areas is the strip of the last rectangle from 4 to 4.5. If you integrate 1 * 2x from 0 through 4.5 you get 31.20, much closer to 31.
In your original problem the strip under the curve from 30 to 30.5 is very large. When I calculated the integral of .01 * 2x from 0 through 30.5 I got $21,907,327.79.
I hope this helps,Harley