Subject: summation problem

My name is otoniel. The level of the problem is precalculus. Here it is:

Without using mathematical induction, or any other method discovered after 1010 a.d. , prove that the sum of i³, (where i, is the index of summation) from one to, n, is equal to ((n*(n+1))/2)².

I am not sure what exactly you are able to use but I can point you in the direction of a proof that does not use mathematical induction. First you need to know that for each positive integer k

Next consider the (1+2+3+...+n) by (1+2+3+...+n) square

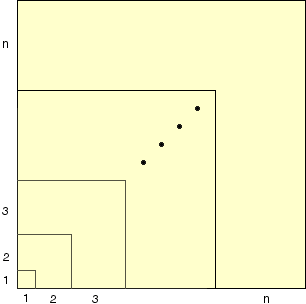
and find the area of each of the L-shaped regions.