I have been working on this problem for some time. It was presented as a trigonometry problem that can be solved using cosine. The best approach I have come up with is outlined below. The person who posed the problem has left my distinct. I am attempting to contact him for a solution or hints leading to a solution.

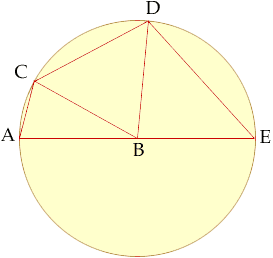
AE is a diameter of a circle and AC, CD and DE are chords of lengths 1, 2 and 3 respectively. (See the diagram.) Find the ridius of the circle.

Each triangle ABC, CBD and DBE can be divided in half forming right angle triangles. (B is the center of the circle.)

The problem can then be solved using cosine and simultaneous equations, I think.

Qustion submitted by Paul, secondary year 11 level qustion. I am a parent trying to help my children with their homework.

Hi Paul,

Your idea for approaching this problem does lead to a solution.


Suppose that the radius of the circle is r. Construct a perpendicular from B to each of the line segments AC, CD and DE as in the diagram below.

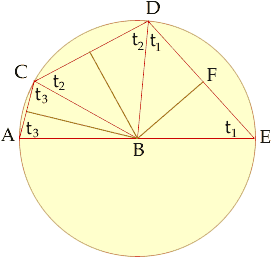
Consider traingle DBE. Let t1 be the angle measurement of angle BED then

Angle DBE + t1 + t1 = 180o Simularly Angle CBD + t2 + t2 = 180o and Angle ABC + t3 + t3 = 180o But Angle ABC + Angle CBD + Angle DBE = 180o and hence t1 + t2 + t3 = 180o

Again considering triangle DBE, |ED| = 3 and hence |EF| = 3/2. Thus

cos(t1) = |EF| / |BE| = ( 3/2)/r Simularly cos(t2) = 1/r and cos(t3) = ( 1/2)/r

Since t1 + t2 + t3 = 180o,

cos(t1)

= cos(180o - (t2 + t3))

= - cos(t2 + t3)

= - [cos(t2) cos(t3) - sin(t2) sin(t3)] Thus 3 = 2r cos(t1)

= - 2r [cos(t2) cos(t3) - sin(t2) sin(t3)]

Simplification of this equation leads to

2 r3 - 7r - 3 = 0 At this point the best that I can do is to approximate a solution. Doing so I find that r = 2.05655

I hope this helps,
Harley
Go to Math Central