Joey
secondary student

I have tried many different avenues but have gotten nowhere on this problem, any help would be much appreciated.

The figure shows a lamp located three units to the right of the y-axis and a shadow created by the elliptical region x² + 4y² < 5. If the point (-5,0) is on the edge of the shadow, how far above the x-axis is the lamp located? Thanks a lot.

In the diagram I have labeled as P the point where the line joining the light to (-5,0) touches the ellipse. If you can find the equation of this line then the height of the light is the y-coordinate of the point on the line with x-coordinate 3.

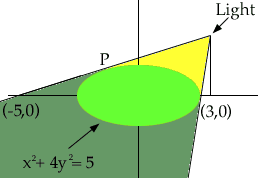
The line joining the light to (-5,0) is tangent to the ellipse and hence its slope can be found from the equation x² + 4y² = 5. First find the function f(x) which describes the top half of the ellipse by solving the equation for the ellipse for y. (Choose the positive sign for the square root since P is on the upper half of the ellipse.) This gives

and hence

Suppose that the first coordinate of the point P is a, then P has coordinates . Thus the line joining the light to (-5,0) has slope f'(a) and passes through . Write the equation of this line. Since the line passes through (-5,0), substitute x = -5 and y = 0 into this equation and solve for a.

Once you have a you can write the equation for the line joining the light to (-5,0) and substitute x = 3 to find the height of the light.