Name: rajesh

Question:
A man goes out in time between 5 and 6 and when he comes back he observes that two hands have interchanged position. Find when the man did go out?

I have changes the numbers on the clock in the diagrams below so that they read minutes rather than hours. When the man went out the hour hand was between 5 and 6, that is 25 and 30 on the diagram. I am going to assume that the hands don't cross between the time he leaves and the time he returns so, when he goes out, the minute hand is between 30 and 35.

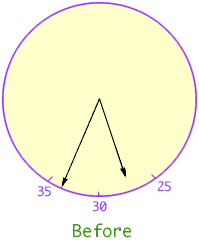
When the man returns the minute hand and the hour hand have changed position.

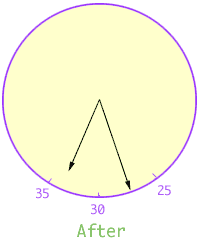
Looking at the "after" diagram again, the minute hand has gone the distance described by the red arc below and the hour hand has gone the distance described by the green arc.

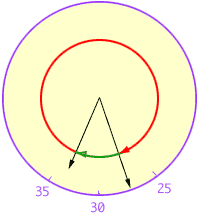
But the minute hand moves 12 times as fast as the hour hand so the red arc is 12 times as long as the green arc. Suppose that the length of the green arc is s minutes then the length of the red arc is 12s minutes. But s + 12s = 60 minutes so s = 60/13 minutes which is approximately 4.6 minutes.

Finall look at the clock midway between the time the man went out and the time when he returned.

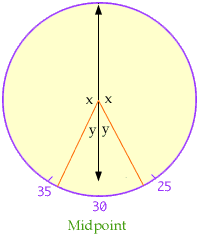
The hour hand has moved halfway from its starting to ending positions and the minute hand has moved halfway from its starting to ending positions. Thus the angles marked x in the diagram are equal and the angles marked y in the diagram are equal. Hence the hour hand and the minute hand form a straight line and therefore the time is 6:00. Hence at the time the man left the minute hand is in the position 30 + ¹/₂(⁶⁰/₁₃) and the time is approximately 5:32.

One last point is that there are other answers to this problem where the hands cross before the man returns.