Subject: Trig question
If x is in radians, how do you solve for x, where: x-sin(x) = constant?
Keith Roble
secondary
other (professional)
I know of no way to directly solve this equation, the best you can do is approximate a solution. The most widely used technique is Newton's method, or sometimes called the Newton-Raphson method. This technique applies to equations of the form f(x) = 0 where f(x) is a differentiable function and requires the function f(x) and its derivative f'(x). The procedure progresses through a seuqence of steps.
- First you need a initial approximation, x1 to the solution
- Calculate a second approximation using the expression
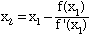
- Calculate a third approximation using the expression
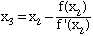
- In general, at each step calculate the next approximation using the expression
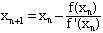
In many situations the sequence x1, x2, x3, ... will converge to a solution of the equation f(x) = 0.
For your problem suppose that the constant is C and then the equation x-sin(x) = constant can be written f(x) = 0 where
Here, f'(x) = -1 + cos(x) and the iterative step is given by
I tried this technique with C = 10 and x1 = 10 with the following results
| n | xn | f(xn) |
|---|---|---|
| 1 | 10 | -0.54402 |
| 2 | 9.70419 | 0.02003 |
| 3 | 9.71440 | 0.00001 |
You need be careful when applying Newton's method. In particular it is sensitive to the initial approximation x1. For some values of x1 the sequence may not converge, or may converge to a solution which is different from the solution you are seeking. I suggest that you find a reference on Newton's method. You can find it in most Calculus books.
Cheers,Harley