Geometry problems involving triangles

Subject: geometry problems involving triangles

Name: Sandi

Who is asking: Student
Level: Secondary

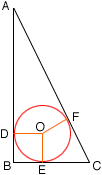
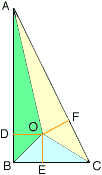
Question: Find the radius of the largest circle contained in a right triangle whose legs are 8 and 15 and hypotenuse is 17. If the right triangle has legs a and b and hypotenuse c, find an expression for the radius of the circle.

Hint: use the area of a triangle (Area = 1/2bh)

The triangle inequality guarantees that the sum of the lengths of two sides of a triangle is greater than the length of the third. As a consequence, if x and y are the legs of a right triangle, with x less than or equal to y, and z the hypotenuse, then x + y is greater than z, so x is greater than z - y. UNDER WHAT CIRCUMSTANCES WILL x is greater than 2(z - y) be true?

THANK YOU VERY MUCH FOR YOUR HELP.

Hi Sandi,

Let triangle ABC be the right triangle with |AB| = 15, |BC| = 8 and |CA| = 17. In the diagram below the largest circle contained in the triangle has center O.

This circle must be tangent to the sides of the triangle at D, E and F and hence angle ADO, BEO and CFO are right angles. Join AO, BO and CO to get the diagram below.

Now use the fact that the area of the triangle ABC is the sum of the areas of the triangles ABO, BCO and CAO and each of the interior triangles has height which is the radius of the circle.

I hope this helps,
Penny Go to Math Central