Name: Sarah

Who is asking: Parent
Level: Secondary

Question:
Cut out of paper or cardboard a quadrilateral having no two sides parallel, no two sides of equal length and no indentations. Can an endless floor be tiled with copies of such a figure?

Please include diagrams if necessary.

Thanks in advance,

Sarah

Sarah replied "I appreciate the diagram, yet would like to know how you approached this question."

At first I was not sure if it would be possible to tile the infinite plane with an irregular quadrilateral. In fact, I tought that it would be impossible. So I wanted to look at tilings with quadrilaterals to find a pattern which would force either two sides to be parallel or two sides to be of equal length.

The tilings I looked at were subdivisions of other well-known tilings. For instance, the plane can be tiled with regular hexagons; I subdivided the regular hexagon into quadrilaterals as follows:

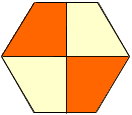
By repeating this pattern, you get a tiling with quadrilaterals of 4 different side lengths, but with two sides parallel. I next looked at subdivisions of the square into 4 quadrilaterals with no two sides parallel:

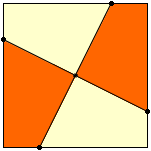
Joining the 4 points marked with a dot to the center, you subdivide the square into 4 quadrilaterals with no two sides parallel, though they have sides of equal length.

At this point I began to have problems with my original assumption: Seeing that these examples were so different, and also by analogy with other geometric problems, I began to suspect that if the construction was indeed impossible, then the proof that it is impossible would be very complicated. If this had been the case, you might have gotten a reply in a few days, when our expert in geometry returned from a trip.

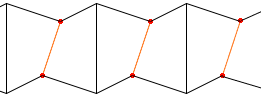
Now the best I could do was to look at other tilings and try to remove the two undesired features at the same time. I started with an infinite ladder:

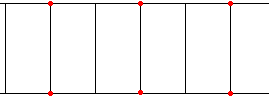
I noticed that by moving the points labeled with a dot inwards, I could get rid of both the parallel sides and the equal lengths.

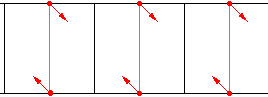
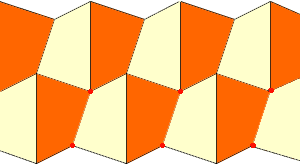
The quadrilaterals would be similar if the displacements were symmetric. I then realized that the angles would also match so that many copies of this ladder could be fitted against each other to tile the whole plane.