Name: Stephanie

Who is asking: Student
Level: Secondary

Question: The three lines PS, PT, and RQ are tangents to the circle. The points S, X, and T are the three points of tangency. Prove that the perimeter of triangle PQR is equal to 2PT. (Diagram: Circle, with tangent line RQ. Attach lines PQ and PR to form a triangle. Line PR extends to PS, creating another tangent. Line PQ extends to PT, creating yet another tangent.) Many thanks if you can help me prove this one!

The problem is not well stated. You need P and the circle to lie on opposite sides of the tangent RQ.

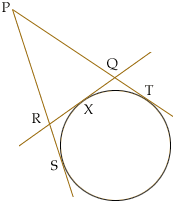
A much better way to state the question:

The proof is easier that the statement -- just use the fact (3 times) that the two tangents from a point to a circle have the same length. For example |PS| = |PT|.