An emergency response station

Who is asking: Student
Level: Secondary

Question:
I don't where to begin! :(

Three cities lying on a straight line want to jointly build an emergency response station. The distance between each town and the station should be as short as possible, so it cannot be built on the line itself, but somewhere east or west. Also, the larger the population of a city, the greater the need to place the station closer to that city. You are to minimize the overall sum of the products of the populations of each city and the square of the distance between that city and the facility. City A is 6 miles from the road's origin, City B is 19 miles away from the origin, and City C is 47 miles from the origin. The populations are 18,000 for City A, 13,000 for City B, and 11,000 for City C. Where should the station be located?

We are told we HAVE to build it east or west of the highway, with the distance minimized from that perspective. Thank you.

Hi Tara,

In the diagram below I put the station at the point F. My understanding of the problem is that you are to minimize the expression

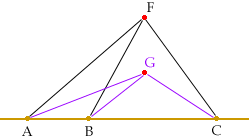
Q = 18,000 |AF|² + 13,000 |BF|² + 11,000 |CF|² where |AF| is the distance from A to F, etc.

Choose any point F not on the line, say east of the line, and calculate

Q1 = 18,000 |AF|² + 13,000 |BF|² + 11,000 |CF|² (In the diagram I have east as up.) Now move F west to the point G, say half the distance to the line. Calculate Q2 = 18,000 |AG|² + 13,000 |BG|² + 11,000 |CG|² But |AG| < |AF|, |BG| < |BF| and |CG| < |CF| so Q2 < Q1.

The point is that no matter where you put F, not on the line, you can always make Q smaller by moving F closer to the line. This argument shows that the location of F that minimizes Q must be on the line.

Cheers,
Claude and Penny Go to Math Central