Name: Tom

Who is asking: Teacher
Level: Secondary

Question:
Consider some squared paper with lines 1cm. apart and dots where the lines cross. Place squares whose sides are whole numbers of centimetres on the paper in such a way that the sides of the squares always lie along the lines on the paper. For each square, find (a)the number of points inside the squares; (b)the number of points on the square and (c)the area of the square. How are these quantities related?

I would draw such a square, count the points inside and on the square to see if I could see a pattern. I am not thinking about a pattern in the numbers but rather in the process. For example consider the square below.

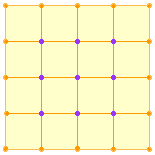
The number of dots along one side is 5 so there are 4 times 5 dots on all 4 sides. This process counts each of the dots twice and hence the total number of dots on the sides is 4x5 - 4. This argument works, regardless of the number of dots on each side. Suppose that the number of dots along one side is n then the number of dots on the square is

To see part (a) notice that dots inside the square form a square array with n - 2 dots on each side.

Try this exercise with a rrectangle rather than a square and then a triangle.

It appears your problem is leading to Pick's Theorem which deals with polygons drawn on a lattice (the "lined paper with dots where the lines intersect" you mention).

Pick's Theorem provides the relationship between the number of lattice points on the boundary of the square and the number of lattice points in the interior of the square to the area of the square. In fact, any polygon drawn on a lattice will exhibit the same relationship. Pick's Theorem can be stated as follows:

Let P be a lattice polygon. Assume there are I(P) lattice points in the interior of P, and B(P) lattice points on its boundary. Let A(P) denote the area of P. Then

A(P) = I(P) + B(P)/2 - 1

There are java applets at various web sites that illustrate this theorem in an interactive way. One such site is Cut-the-Knot at www.cut-the-knot.com/ctk/Pick.html

An alternative is to experiment with geoboards (boards with nails at the "dots" to form a lattice) and elastics.

Hope this helps,
Leeanne and Penny