Name: Wayne

Who is asking: Other
Level: Secondary

Question:
I know that the domain of f'(x) is a subset of the domain of f(x). Is it necessarily true that the subset will have at most one less element than the domain of the original function? Thank you

Hi Wayne,

The domain of f'(x) is a subset of the domain of f(x) as you mentionsd, but the difference can be more than one point. The first function that I show my students of a continuous function that is not differentiable is f(x) = |x|.


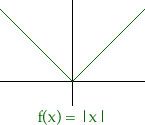
Here the domain of f(x) is all the real numbers and the domain of f'(x) is all the real numbers except 0. It is the "corner" in the graph at (0,0) that creates the difficulty.

To construct a function that has more than one point where the derivative does not exist you can create a function with more that one "corner". One such function is

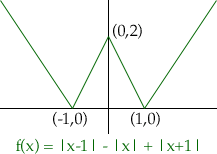
f(x) = |x - 1| - |x| + |x + 1| Its graph has 3 "corners", and hence three points where there is no derivative.

In fact you could construct a function whose graph looks like the teeth on a saw of infinite length, and which then has no derivative at infinitely many points.

I hope this helps,
Harley
Go to Math Central