Name: alyaa

Who is asking: Student
Level: Secondary

my question is :
a marquee with rectangular sides on a square base with a flat roof is to be constructed from 250 meters square of canvas. find the maximum volume of the marquee. i find this topic so hard, so please if you help me with this topic i will be blessed if you send it to me and answer my question. thank you very much



Hi Alyaa,

The problem, the way it is worded, does sound confusing. You are to make a marquee out of canvas. It has rectangular sides, a square base and a flat roof. So it's "box shaped". Does it have a base made of canvas? I don't know. I looked in my dictionary and it is not clear. I am going to assume that it has no base. If it does have a base you will have to modify my solution. Hence what I see is five pieces of canvas put together to form a box, the four side pieces are rectangular and the roof os square. I need dimensions so I am going to say that the roof is x meters by x meters and the height of each side is y meters. Here is what I see.


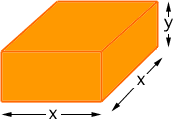
And here are the five pieces.

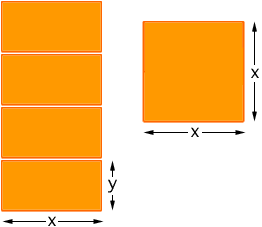
The problem says that the marquee "is to be constructed from 250 meters square of canvas". What this means is that the total area of the 4 sides and roof is 250 square meters. The roof is x meters by x meters, hence its area is x 2 square meters. Each of the sides is x meters by y meters and hence each side has area xy square meters. There are 4 sides and thus the total area is

x 2 + 4xy square meters. Thus we know that x 2 + 4xy = 250 or y = (250 - x 2)/4x.

The quantity you want to maximize is the volume of the marquee. The volume of a box is length times width times height and thus the volume of the marquee, V, is given by

V = x 2 y cubic meters Substituting y from the previous equation gives V = x 2  (250 - x 2)/4x = 1/4 (250x - x 3)

Can you solve the problem now?

Harley

Go to Math Central