Name: Ashlie

Who is asking: Student Level: Middle

Question:
How do you find the chord length of one section of a chord if you only have the diameter length and the other whole chord length.

WV is the diameter and equals 16. XY is perpendicular to it, and equals 10. They intersect at pt. Z. I need to know what WZ equals. Please help!



Hi Ashlie,

In the diagram below I let x be the length of WZ and then the length of ZV is 16 - x.

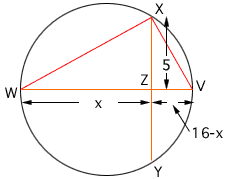
The important geometric fact here is that triangles XWZ, XZV and XWV are all right triangles. Thus, by the theorem of Pythagoras, |WZ| 2 + |ZX| 2 = |XW| 2
|XZ| 2 + |ZV| 2 = |VX| 2 and
|VX| 2 + |XW| 2 = |WV| 2 That is x 2 + 5 2 = |XW| 2
5 2 + (16 - x) 2 = |VX| 2 and
|VX| 2 + |XW| 2 = 16 2 Solve for x.

Penny

Go to Math Central