Hi,
I am a student in a college level Calculus 1 class. Here is my question...
A spotlight on the ground shines on a wall 12m away. If a man 2m tall walks from the spotlight toward the bldg at a speed of 1.6 m/s, how fast is his shadow on the bldg decreasing when he is 4m from the bldg?
I have been trying to figure this out for quite some time and now it is due very soon and I still do not have the answer! I know I'm supposed to use similar triangles and set up a proportion equation and then take the derivative, but can't get the equation. Any help that you could provide would be greatly appreciated. Thank you very much,
Barb
Hi Barb,
The first thing to do is to draw a diagram and label the quantities that don't change. Here what doesn't change is the height of the man and the distance from the spotlight to the wall. Give variable names to the important quantities that change. Here the height of the shadow is important since the question asked is about this height. I am going to call this height h(t). The height of the shadow is changing so it is a function of t. The distance from the man to the spotlight is also importand since you are given the rate at which this distance is changing. Call this distance x(t). Again it is a function of t. Thus my diagram is:
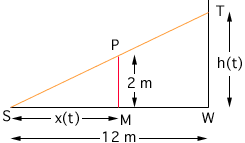
The spotlight is at S, the man at M, the top of his head at P, the base of the wall at W and the top of the shadow at T.
The similar triangles are PSM and TSW. Thus
Penny