Name: Brandie

Who is asking: Teacher
Level: All

Question:
Could you please tell me what is the basic guideline for inverting a function

Example:
S(R)=2PiRal
V(R)=PiR(squared)bl
R(V)=?

help please I am stuck... Thank you!

For V(R) = Pi*R(squared), you proceed as follows:

1. Suppose the function is written on the x-y axis, with x = R and y = V(R):
   
   y = Pi*x²
   
   
2. Solve for x (that is, isolate x):
   
   y/Pi = x²
   
   
   
   
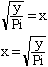
3. Now your x is R(V) and y is V:
   
   

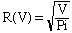
That's it, you have inverted the function. It becomes easy once you get the hang of it. Mathematicians think, in the first case, of V(R) as being a function of the independent variable R, and in the second case of R(V) as a function of the independent variable V. The name given to a variable is not important: You could as well write V(x) = Pi*x² or V(t) = Pi*t(squared) or so on, and it would mean the same as V(R) = Pi*R² (just like subroutines incomputer programs). However it is very important to write V(x) rather than just V, to indicate that it is a function in that variable.

Physicists have a different viewpoint. They would simply write V = Pi*R² and view it as a relation between the quantities V and R. of course this relation is the same as the one expressed by the equation R = square root of{V/Pi}, that is, they may not see the point of making such a big fuss about "inverting functions". On the other hand they do not like to change the name of their variables: t should always mean time, T temperature, and so on.