I own a piece of property that I need to know the square feet for assessment purposes. The figure they came up with is wrong. They measured from one point to another and halved the sums but that means I own the cul de sac and we don't. My lot is 55 feet wide and one side is 108.96 feet and the other side is 146.04 that extends all the way to a circle. The front of the lot on the cul de sac is stated on the survey like this. 78.21 feet where R=40 feet. This large arc is taken off the size of our land. How many square feet is our lot.

Thank you.
Claudia (private party)

Hi Claudia,

From your description I have the diagram below. Here C is the center of the circle of radius 40 feet as stated in the survey. To find the area of your lot you need to do some trigonometry.


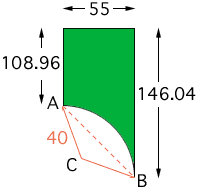
The length of the arc from A to B, 78.21 feet is given by
78.21 = R x theta Where R is the radius of the circle (40 feet) and theta is the angle measurement in radians. Thus
theta = 78.21/40 = 1.95525 radians.

The length of the line AB (the base of the triangle ACB) is

2 x 40 x sin( theta/2) = 2 x 33.1669 = 66.3338 feet The height of the triangle ACB is
40 x cos( theta/2) = 22.3957 feet Thus the area of the triangle ACB is
 1/2 x 66.3338 x 22.3597 = 741.603 square feet

The area of the sector of the circle bounded by the lines AC and CB and the arc from A to B is

R2 x theta/2 = 402 x 1.95525/2 = 1564.2 square feet. Thus the area of the crescent shaped region bounded by the line AB and the arc of the circle is
1564.2 - 741.603 = 822.597 square feet. Hence the area of your lot is
55 x (108.96 + 146.04)/2 - 822.597 = 7012.5 - 822.597 = 6,190 square feet.

Harley
Go to Math Central