Good Day:

The question I have is for figuring the distance from one planetary object to another. I suppose it could be middle or secondary for status, as I don't know what level of math is taught when. I also guess I would classify as an 'other'.

The question is: how do I figure out the distance of one object in 3D space to another object in 3D space? I have an object at say x = 5.872, y = 2.876, and z = 7.290; and the other object is at x = 1.129, y = -8.213, and z = -11.127. I have been suggested to use the pythagorean theory on this, but since there are three variables, I don't understand how.

David

Hi David,

Suppose that you have two points A and B in 3-space as in the diagram below.

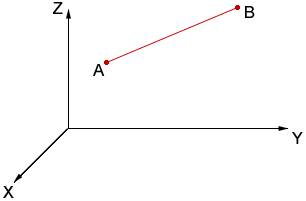
Construct a rectangular box with edges parallel to the axes and with the line AB a diagonal of the box as in the diagram below.

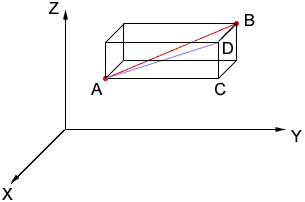
Since the triangle ADB is a right triangle, the theorem of Pythagoras gives

|AB|2 = |DB|2 + |AD|2 Also, since the triangle ACD is a right triangle, |AD|2 = |AC|2 + |CD|2 Hence |AB|2 = |DB|2 + |AC|2 + |CD|2

If A = (x1, y1, z1) and B = (x2, y2, z2) then C = (x1, y2, z1) and D = (x1, y2, z2) and

|AB|2 = (x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2

Cheers,
Penny

Go to Math Central