Subject: Third side of Acute Triangle
Hello,
I gave this problem to my children, 9th and 12th grade and they are not(me too!) sure of the answer. I am trying to determine the length of the third side of an acute triangle. I know two of the lengths but I do not know the angles. Is there a proper formula to use to find the length of the third side? Thank you.
Don
Father of Rachel and Evan
Knowing the lengths of two sides of an acute triangle does not determine the length of the third side. For example you have a triangle with side lengths L and S with S <= L and T is the length of the third side. If the angle between the sides of length S and L is very small (close to zero) as in the diagram below, then T is only slightly larger then L - S. (If L = S then T is almost zero.)
If, on the other hand, the angle is 90o as in the second diagram then the Theorem of Pythagoras tells us that T =
. Since the triangle is acute, the angle must be less than 90o, but it might be very close to 90o.
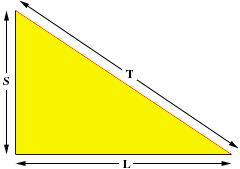
Thus the best you can say is that
If you know the angle between the sides of lenght L and S you can use the Law of Cosines to find T. Chris and Penny