Name: Eric

Who is asking: Other
Level: Secondary

Question:
How can I solve |x + y| + |x - y|< =6?

You can solve this problem by considering 4 cases which depend on the values of the quantities inside the absolute value symbols. These are.

1. x + y >= 0, x - y >= 0 and |x + y| + |x - y|< =6
   
   
2. x + y >= 0, x - y < 0 and |x + y| + |x - y|< =6
   
   
3. x + y < 0, x - y >= 0 and |x + y| + |x - y|< =6
   
   
4. x + y < 0, x - y < 0 and |x + y| + |x - y|< =6

x + y >= 0 is equivalent to y >= -x. I see this inequality graphically. I see the line y = -x in the plane, and y >= -x describes all the points on one side of the line. To determine which side I take one point in the plane, not on the line, say (0,1). The point (0,1) satisfies the inequality y >= -x and hence (0,1) is on the side of the line described by the inequality. In the diagram below I have shaded in rred the points in the plane that satisfy the inequality. Notice that this includes the liny y = -x.

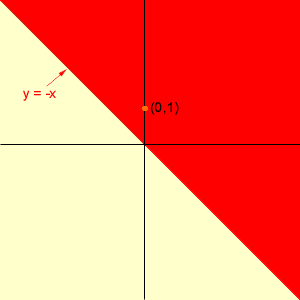
x - y < 0 is equivalent to x < y. Here the bounding line is y = x. Since (0,1) satisfies the inequality, (0,1) is on the side of the line described by the inequality. Again this is the region shaded in red in the diagram. This time points on the bounding line y = x do not satisfy the inequality.

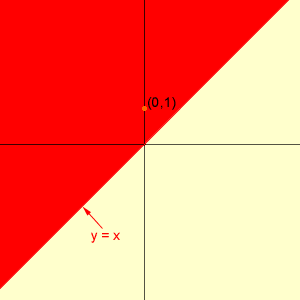
For a point (x,y) to satisfy the first two conditions for case 2 it must lie in both regions shaded red. Thus the portion of the plane that satisfies the conditions for case 2 are the points shaded red in the diagram below.

Finally, to complete case 2 we need to which of the points identified above satisfy the inequality |x + y| + |x - y|< =6. Since x + y >= 0, |x + y| = x + y. Since x - y < 0, |x - y| = -(x - y). Thus the inequality becomes

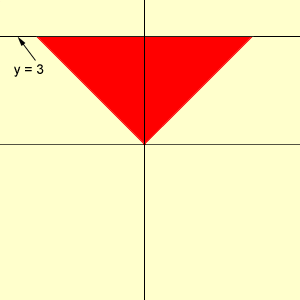
Now try the other 3 cases. The points that satisfy the inequality |x + y| + |x - y|< =6 are the points that satisfy any of the three cases.