Hi my math teacher asked us to solve an augmented matrix. I am in twelfth grade and need help. The book we are working on is college algebra. Here it is

a+2b+c=0
2a+5b+4c=-1
a-b-9c=-5

Thank you for your help



Hi,

The augmented matrix is formed by taking th matrix of coefficients and "augmenting it" by appending a column containing the numbers on the right side of the equations. For your problem the augmented matrix is

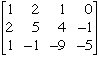
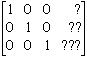
The goal is to perform legitimate operations on this matrix to transform it to the form since this is the augmented matrix for the equations a = ?
b = ??
c = ??? which is the solution you are looking for.

Start with the first column. I would like to transform the 2 in the second row to 0. To do this I will multiply the forst row by -2 and add it to the second row. (If you think in terms of the equations you started with, this is multiplying the first equation by -2 and adding it to the second equation.) Performing this operation gives

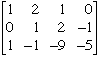
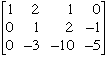
Continuing with the first column, I can transform the 1 in the third row to 0 by multiplying the first row by -1 and adding it to the third row. Thus I get

The first column is now in the form I want so I can now turn my attention to the second column. I want the -3 in the third row to be 0 and I can arrange this by multiplying the second row by 3 and adding it to the third row. This gives

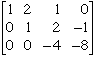
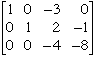
Similarly if I multiply the second row by -2 and add it to the first row I get

Finally the third column. I want the entry in the third row of the third row to be 0 rather than -4. To accomplish this I multiply the third row by - 1/4. (This is the same operation as multiplying both sides of an equation by - 1/4.) The resulting matrix is

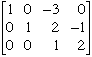
I leave it to you now to complete the problem by transforming the third column into the desired form.

A nice feature of this problem is that you can verify your answer. Once you have values for a, b and c you can substitute them into the original equations to see if they are valid.

Cheers,
Penny

Go to Math Central