Subject: Volume
My name: Jason
Difficulty level: College
I am a high school math teacher. I was asked by a friend who is in architectural design for a method for determining the volume of what he called a Catenary.
The Catenary curve is modeled by the equation y=a cosh(x/a). I ran into a mess when I tried to compute the volume of the solid formed by revolving that curve around the y-axis.
Any help you can provide would be greatly appreciated.
Jason
Hi Jason,
The catenary is a very interesting curve. It is the shape taken by a flexible cable (like a power line) suspended between two towers of the same height. The name comes from the Latin word for chain.
I am going to assume that the piece of the catenary that you want stetches form -b to b on the x-axis. In the diagram below then you want to revolve either the region shaded red or the region shaded blue around the y-axis. If you can find one volume you can find the other since their sum is the volume of a right, circular cylinder.
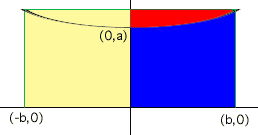
I am going to find the volume obtained by revolving the region shaded blue around the y-axis. This is the region bounded by
y = 0
x = 0 and
x = b
Take a strip of thickness delta-x, at r on the x-axis, as in the diagram and rrevolve it about the y-axis.
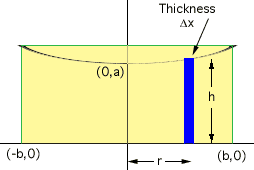
This gives a cylindrical shell of radius r, height h and thickness delta-x, and hence volume
The volume required is thus
You can evaluate this integral using integration by parts with
dv = cosh(x/a) dx
Harley