hi. there's a problem my calculus teacher gave that I cannot solve....

A lighthouse at apoint P is 3 miles offshore from the nearest point O of a straight beach. A store is located 5 miles down the beach from O. The lighthouse keeper can row at 4 mph and walk at 3.25 mph.

a)How far doen the beach from O should the lighthouse keeper land in order to minimize the time from the lighthouse to the store?

b)What is the minimum rowing speed the makes it faster to row all the way?

I think the problem would only make sense if he rowed slower than he walked, or else he would have rowed the whole way, right? If I made row=3.25 mph and walk=4 mph, how would I answer part b)? By the way, the answer I got for a) was 4.18 m down the beach. Is it correct? thanks

I agree. The shortest distance from lighthouse to the store is the straight line (rowing all the way) so if he can row faster that he can walk, or even row and walk at the same rate, then the shortest time would be obtained by rowing all the way.

I changed the problem to make him row at 3.25 mph and walk at 4 mph and found the minimum time when the distance down the beach is 4.18 m, as you did. I set it up as in the diagram. I assume that you did something similar.

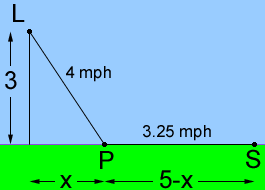
To approach problem b) I let his rowing speed be r mph and his walking speed be w mph and solved the the problem again, exactly as I did with the values 4 mph and 3.25 mph. I arrived at