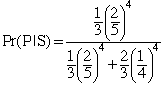Sender: Kate
There is a great debate among my friends regarding the answer to this question:
Suppose Stock Brokers tell the truth 2/5 of the time, and 1/3 of the trees in a given forest are Pine. If 4 Stock Brokers say that a certain tree in that forest is Pine, what is the probability that the tree is indeed a Pine tree?
Could you please show us how to solve this? Thanks!
Hi Kate,This is a conditional probability problem. The problem is to find the probability that the tree is a pine given that 4 Stock Brokers say that it is a pine. To save on typing let P be the statement "The tree is a pine." and S the statement "The 4 Stock Brokers say that the tree is a pine." The problem is thus tio find Pr(P|S).
The rules of probability say that
I would find these probabilities using a tree diagram. At the bottom level the tree is either a pine tree or it is not a pine tree. The probability that it is a pine tree is 1/3 so the probability that it is not a pine tree is 2/3.
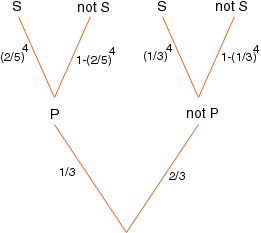
If the tree is a pine tree then the probability that all 4 Stock Brokers say that it is a pine is (2/5)4. If the tree is not a pine tree then the probability that all 4 Stock Brokers say that it is a pine is (1/3)4.
Pr(P and S) is thus 1/3( 2/5)4 and Pr(S) is 1/3( 2/5)4 + 2/3( 1/3)4.
Hence